The Gram-Schmidt process takes a set of N vectors or functions and an inner product. It then builds a set of N orthogonal vectors/functions from the original ones. It is a process that can be easily automated using symbolic calculations.

This is done using Mathematica in this notebook. It begins with defining the inner product as a Mathematica function:

ip[u_, v_] := Integrate[u v, {x, 0, X}]

In this case the inner product is the integral of u(x) times v(x) from 0 to X. We then define the set of functions (vectors in our vector space):

u = {x^2 - X^2, x^2 (x - X), x^2 (x - X)^3}

This line and the one for the inner product are the only lines that need to be edited by the user.

In this case our functions are \( x^2 – X^2\), \(x^2 (x – X)\) and \( x^2 (x – X)^3 \).

We then create a list to store the orthogonal functions:

v = Table[i, {i, 1, Length[u]}]

This is followed by a for loop that computes the Gram-Schmidt procedure, simplifies the output, and then normalizes the function:

For[i = 1, i <= Length[u], i++,
 v[[i]] = FullSimplify[u[[i]] - Sum[ip[u[[i]], v[[j]]]/ip[v[[j]], v[[j]]] * v[[j]], {j, 1, i - 1}]];
 v[[i]] = FullSimplify[v[[i]]/Sqrt[ip[v[[i]], v[[i]]]]]]

The file also has some lines to output the functions in LaTeX and plot the functions, but those are not essential to the Gram-Schmidt procedure.

For this particular problem, the orthogonal (and orthonormal) functions are

$$\frac{15 (x-X) (x+X)}{8 X^5},$$ $$\frac{84 \left(32 x^3-35 x^2 X+3 X^3\right)}{13
X^7},$$ and $$\frac{6930 \left(2730 x^5-8190 x^4 X+7987 x^3 X^2-2575 x^2 X^3+48
X^5\right)}{1601 X^{11}}.$$

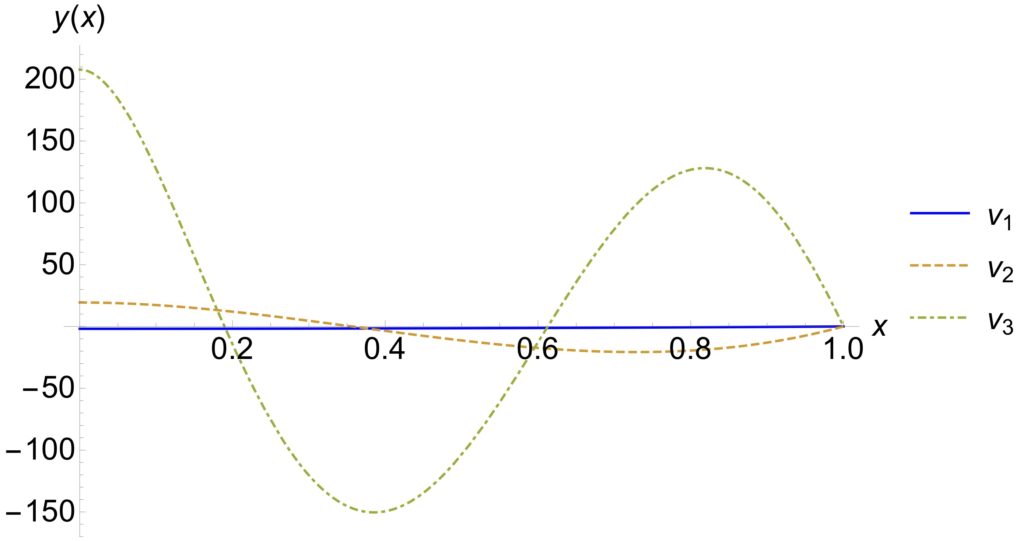
Here is a plot of the functions: